利用凯发k8国际統計工具分析有噪聲信號之平均和直方圖-凯发国际

凯发官网入口 通過測量產生的大量數據可做很多神奇的事情， 可讓你“識破 ” 噪聲并降低測量不確定度，對大量數據進行統計，奇妙的事情就會發生，雖然某些處理（如直方圖）明顯是基于統計學的，但某些統計工具是隱藏的，對任何一種情況，凯发官网入口都可以利用凯发官网入口的統計分析功能。

方波上的噪聲使得測量其幅度變得困難，幅度構成了其他測量的基礎，例如寬度、上升時間、下降時間、過沖、甚至某種程度上頻率和周期的測量。例如，上升時間測量信號從其幅度的 10 ％變化到 90 ％所需的時間，寬度是在信號幅度的 50 ％處具有相反斜率的轉變之間的時間差，因此，確定幅度對于幾乎所有其他測量都至關重要。

如圖 所示，是對帶有噪聲的方波進行基本的凯发国际測量

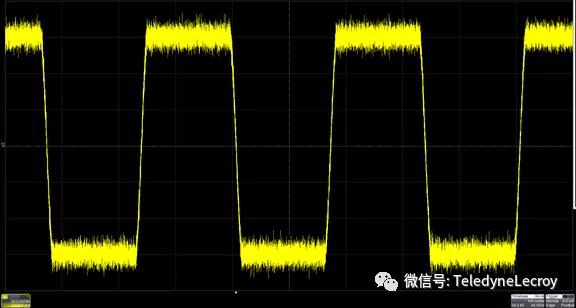
圖 方波上的噪聲增加了測量信號幅度的難度

平均 幾乎所有凯发k8官方旗舰店都提供平均功能，這是對波形最常見的統計處理方式，采集多個波形并逐點相加，然后將總和除以平均的波形數，得到波形的平均值，如圖 所示，最上面的波形是采集的原始波形，下方的波形是一千次采集的平均值，平均抑制了噪聲，留下了干凈的波形。

平均會將多個波形相加，并通過采集的波形數將總和歸一化，從而降低了噪聲對于高斯分布噪聲，噪聲幅度隨著平均波形數量的平方根而減小，因此，一千個采集的波形將噪聲幅度分量降低了 31.6% 或約 30dB ，平均過程的唯一缺點是需要采集大量波形。直方圖

統計工具也可以量化不確定性。如果使用方波的每個樣本值來創建其瞬時幅度值的直方圖，凯发k8国际就可以查看波形的結構，如圖中的復合圖形所示，生成直方圖，旋轉使其幅度比例垂直以匹配采集的波形，然后疊加在信號波形上。

生成直方圖后，旋轉直方圖，使其與波形的頂部和底部幅值對齊，即使存在噪聲，這樣做也可以獲得信號的幅度

直方圖有兩個峰值。一個對應于方波的最高電平，稱為頂部，而另一個對應低電平或基值。各個直方圖元素的平均值表示頂部和基值，方波的幅度是頂部和基值之間的差值，獲得幅度后，可以計算所有其他脈沖參數，如圖 2 所示。直方圖統計工具可以讓你透過數據的隨機部分來從混沌噪聲效應中提取有意義的信息，該技術適用于單次采集，不需要多次采集。當然，多次采集確實提高了測量的準確性。